자료구조(java) 1_2. 빅 오 표기법

1-2. 빅 오 표기법

어떤 알고리즘을 다른 알고리즘과 비교해서 표현하기 위한 표현방식 : 빅 오 표기법(Big Oh Notation).

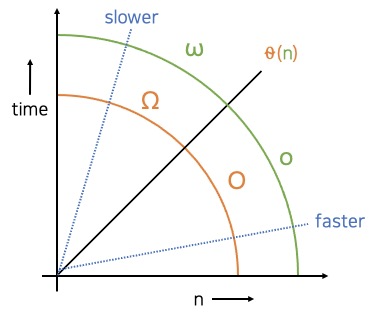
아래 그래프는 복잡도가 n인 알고리즘을 표현.

필요한 일, 메모리 또는 시간을 의미하는 y축.

작업 진척도를 나타내는 x축.

• 빅 오 복잡도 (O) : 비교하고자 하는 다른 알고리즘과 같거나 더 빠른 것을 의미한다.

• 리틀 오 복잡도 (o) : 다른 알고리즘과 빠르지만 같지는 않다.

• 세타 복잡도 (θ) : 비교 대상인 그래프가 일치할 때, 비교 대상인 다른 알고리즘과 같다.

  (같은 정도로 증가하는 것을 의미.)

• 빅 오메가 복잡도 (Ω) : 같거나 느린 것을 의미한다.

• 리틀 오메가 복잡도 (ω) : 같지 않고 느리다.

생각해보기

\1) 빅 오 표기법을 각각 부등호에 대응하면 어떤 것인가요?

O (빅 오 복잡도) : <=

θ (세타 복잡도) : =

Ω (빅 오메가 복잡도) : >=

o (리틀 오 복잡도) : <

ω (리틀 오메가 복잡도) : >

빅 오 표기법 예시

참/거짓 구분 문제.

문제 1.

​ n^4/3 = O( nlog )

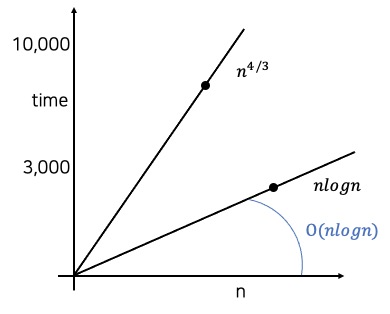
적당히 큰 수 1000을 n에 대입하면, 좌변은 10000이고 우변은 log의 밑이 10일 때 O(3000)이다. 10000은 3000 이하가 아니기 때문에 거짓이다.

문제 2.

​ 3n^3 + 4n^2 + 5n + 6 = θ(n^3)

차수가 제일 높은 항을 제외한 나머지는 무시.

즉 n^3 = θ(n^3) 는 참.

문제 3.

​ n(n−1)/2 = O(n^2)

n^2 = θ( n^2 ) 는 참.

문제 4.

​ 2^n = w(n)

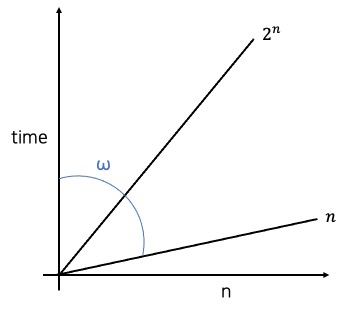
적당히 큰 수인 1000을 n에 대입하면, 2^1000 = ω(1000) . 1000은 1000 이상이기 때문에 이 식은 참이다.

문제 5.

​ n^3 = O(n^2)

n^2는 n^3보다 느리게 증가한다. 거짓.

문제 6.

​ n^2 = O(n^3)

n^2는 n^3보다 느리게 증가한다. 참.

생각해보기

1)문제 1에서 n=1을 대입하면 어떻게 되나요? 적당히 큰 수를 대입해야 하는 이유는 무엇인가요?

알고리즘 복잡도를 계산하는 이유는 많은 데이터를 처리할 때 얼마나 효율적인 알고리즘이냐에 따라서 엄청난 시간적 차이가 생기기 때문.

컴퓨터는 충분히 빠르기 때문에 작은 데이터에 대해서는 사람이 느끼기에 큰 시간적 차이가 아닐 수도 있지만 큰 수 일때는 같은 데이터 양으로도 몇 초만에 풀릴 문제일지, 무한에 가까운 시간이 소요될 지 결정하는 중요한 요소가 되기 때문에 큰 수를 고려하는 것이 의미있는 복잡도 계산이다.

References

자바로 구현하고 배우는 자료구조 -Rob Edwards (boostcourse)